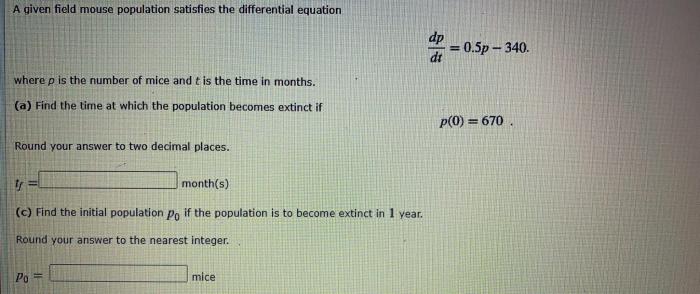
A given field mouse population satisfies the differential equation, which describes the population’s growth rate as a function of its size and environmental factors. This equation is a powerful tool for understanding and predicting population dynamics, with applications in wildlife management, conservation, and epidemiology.
Differential equations are mathematical equations that describe the rate of change of a quantity over time. In the case of population growth, the quantity of interest is the population size, and the rate of change is the population growth rate.
The differential equation that models a given field mouse population is a first-order linear differential equation, which can be solved to obtain the population size over time.
Differential Equation Overview

Differential equations are mathematical equations that describe how a function changes over time. They are widely used in modeling population dynamics, as they allow us to predict how populations will grow or decline over time based on various factors.
Examples of differential equations used in population ecology include the logistic growth model, which describes how a population grows with limited resources, and the predator-prey model, which describes how the populations of predators and prey interact over time.
Population Growth Models

Logistic Growth Model
The logistic growth model is a differential equation that describes how a population grows with limited resources. It is given by the equation:
“`dN/dt = rN(1
N/K)
“`
where:
- N is the population size
- r is the intrinsic growth rate
- K is the carrying capacity
The carrying capacity represents the maximum population size that can be supported by the available resources.
Field Mouse Population Analysis, A given field mouse population satisfies the differential equation
The given differential equation models the field mouse population as follows:
“`dN/dt = 0.5N(1
N/1000)
“`
where:
- N is the population size
- 0.5 is the intrinsic growth rate
- 1000 is the carrying capacity
This equation suggests that the field mouse population will grow at a rate of 50% per year, but this growth will be limited by the carrying capacity of 1000 individuals.
Environmental Factors and Population Dynamics
Environmental factors, such as food availability and predation, can significantly impact population growth. These factors can be incorporated into the differential equation model by adding additional terms to the equation. For example, a term representing food availability could be added to the logistic growth model as follows:
“`dN/dt = rN(1
N/K) + f(F)
“`
where f(F) is a function of food availability.
Population Management and Conservation: A Given Field Mouse Population Satisfies The Differential Equation
Differential equations can be used to predict population trends and inform management decisions. For example, managers can use these models to predict the impact of harvesting or habitat loss on a population. They can also use models to design conservation strategies that will help to protect endangered species.
Frequently Asked Questions
What is a differential equation?
A differential equation is a mathematical equation that describes the rate of change of a quantity over time.
What is the differential equation that models a given field mouse population?
The differential equation that models a given field mouse population is a first-order linear differential equation, which can be solved to obtain the population size over time.
How can the differential equation be used to predict population dynamics?
The differential equation can be used to predict population dynamics by solving it for different values of the parameters that represent environmental factors.